Image Super-Resolution Using Deep Convolutional Networks
24 Apr 2017 | PR12, Paper, Machine Learning, CNN, SRCNN이번 논문은 2015년 IEEE Transactions on Pattern Analysis and Machine Intelligence에 발표된 “Image Super-Resolution Using Deep Convolutional Networks” 입니다.
이 논문은 single image super-resolution (SR) 문제에 최초로 deep learning을 적용한 연구입니다. 이후 거의 모든 super-resolution 연구들이 이 논문에서 제안된 SRCNN을 기반으로 하고 있습니다.
Introduction
SR 문제는 하나의 저해상도 이미지에서 고해상도 이미지를 복원하는 것으로, 하나의 입력에 대해 복수의 결과물이 나올 수 있는 어려운 (ill-posed) 문제로 알려져 있습니다.
지금까지 SR 문제를 풀어 왔던 가장 대표적인 방법은 example-based 방법과 sparse-coding-based 방법이었습니다. Example-based 방법은 저해상도/고해상도 이미지 patch의 쌍을 미리 dictionary 형태로 구축하는 방식이고, sparse-coding-based 방법은 입력된 저해상도 이미지를 sparse coefficient로 encoding했다가 dictionary를 거쳐 복원하는 방식입니다.
Convolutional Neural Networks for Super-Resolution
이 논문에서 입력 저해상도 이미지는 $\mathbf{Y}$, 복원한 출력 고해상도 이미지는 $F \left( \mathbf{Y} \right)$, ground truth 고해상도 이미지는 $\mathbf{X}$로 표현하고 있습니다. 고해상도 이미지를 복원하는 mapping $F$는 아래의 세 가지 연산으로 구성됩니다.
- Patch extraction and representation: 저해상도 이미지 $\mathbf{Y}$로부터 patch 추출
- Non-linear mapping: 다차원 patch 벡터를 다른 다차원 patch 벡터로 mapping
- Reconstruction: 다차원 patch 벡터에서 최종 고해상도 이미지 생성
이 논문에서는 세 가지 연산 모두를 제안하는 Super-Resolution Convolutional Neural Network (SRCNN)으로 처리할 수 있음을 보입니다 (아래 그림). Layer가 3개인 단순한 CNN 구조입니다.
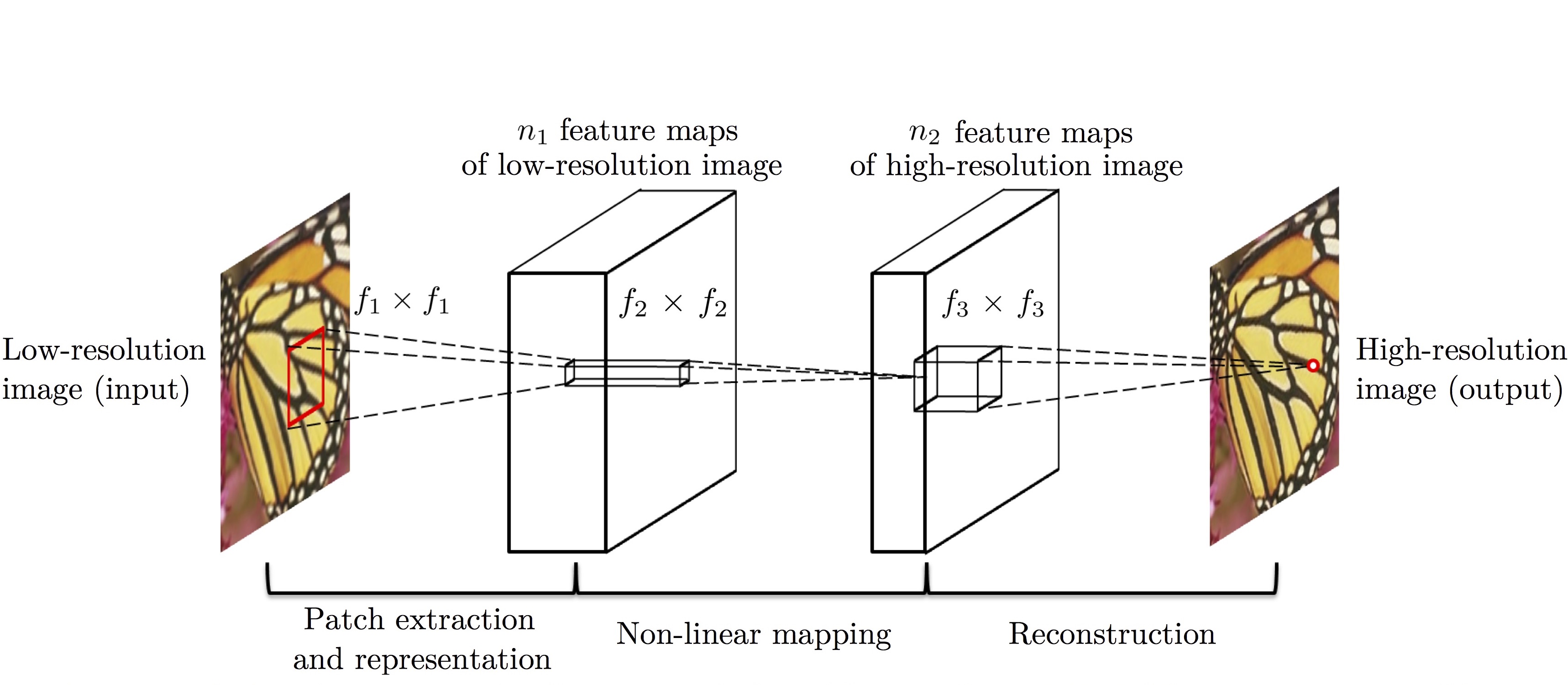
각 layer에서 이뤄지는 연산을 수식으로 표현하면 아래 식과 같습니다.
- Layer 1: Patch extraction and representation
- Layer 2: Non-linear mapping
- Layer 3: Reconstruction
이때, $W_i$는 filter, $B_i$은 bias, ‘$*$’는 convolution operation을 각각 의미합니다. Layer 3를 제외한 Layer 1과 2는 각각 ReLU $\left( \max(0,x) \right)$ 함수를 사용하고 있습니다.
다른 그림으로 이 구조를 보이면 아래 그림과 같습니다. (출처: 전태균 님의 슬라이드)
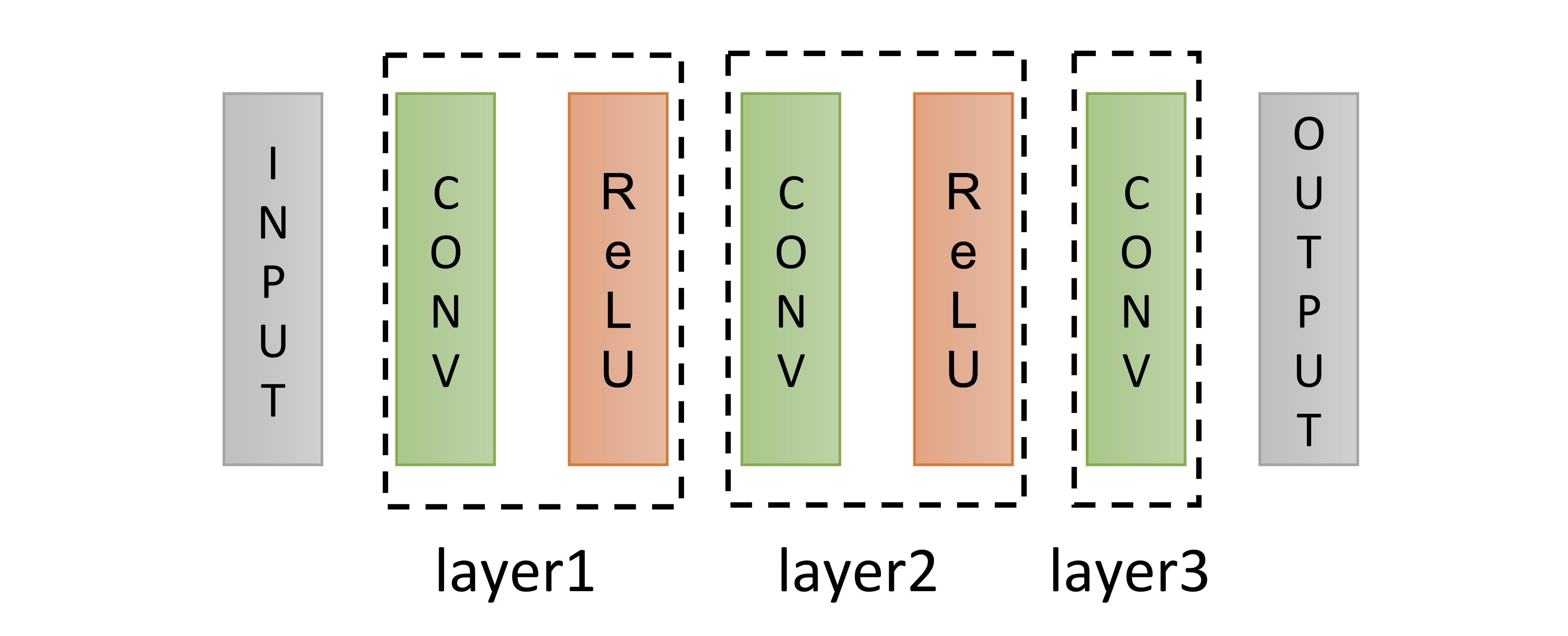
Mapping function $F$의 학습에는 Mean Squared Error (MSE)를 loss function으로 사용합니다.
Experiments
실험 결과를 다른 SR 방법과 비교한 그래프와 출력 이미지를 아래에 보입니다.
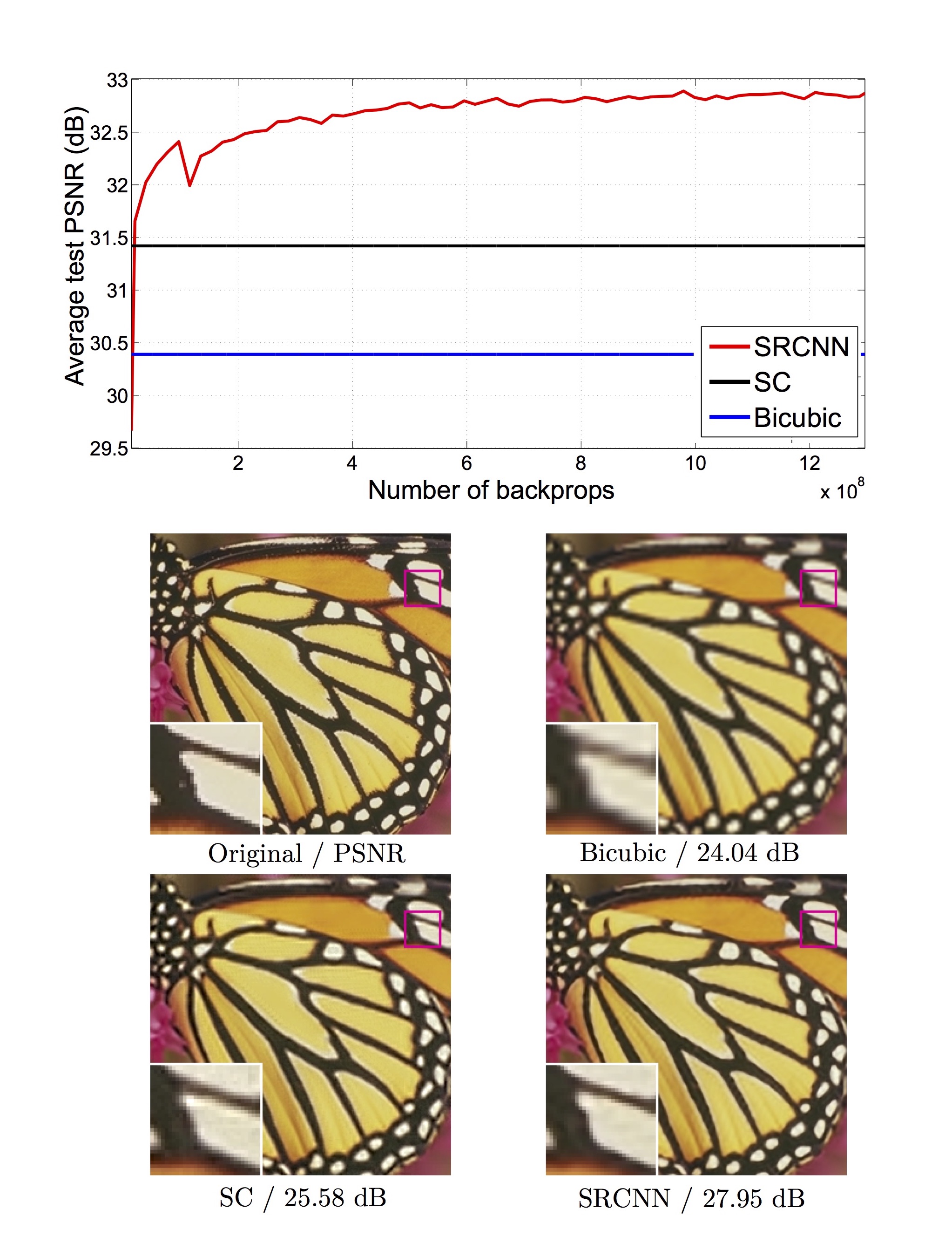
먼저 위 그래프에서 sparse-coding-based 방법이나 bicubic에 비해서 SRCNN의 PSNR이 월등히 높은 것을 볼 수 있습니다. 또한 아래 4개의 나비 날개 이미지에서도 SRCNN이 원본에 비교해도 디테일이 크게 떨어지지 않는 좋은 성능을 보이고 있습니다.
이 실험은 super resolution을 luminance 채널 (YCbCr color space의 Y 채널)에만 적용한 것이지만, 저자들은 이후 다른 실험에서 RGB 모든 채널에 적용하면 성능이 더 좋아짐을 보이고 있습니다.
또한, 더 많은 데이터(ImageNet)로 학습했을 때, 더 많은 필터, 더 큰 필터를 사용하면 역시 성능이 향상되는 것을 볼 수 있었습니다. 한편, CNN의 layer 수를 4개, 5개로 더 늘려도 성능이 더 좋아지지 않는 것이 관찰되었는데 그 이유는 training의 어려움으로 추정하고 있습니다 (아래 그림).
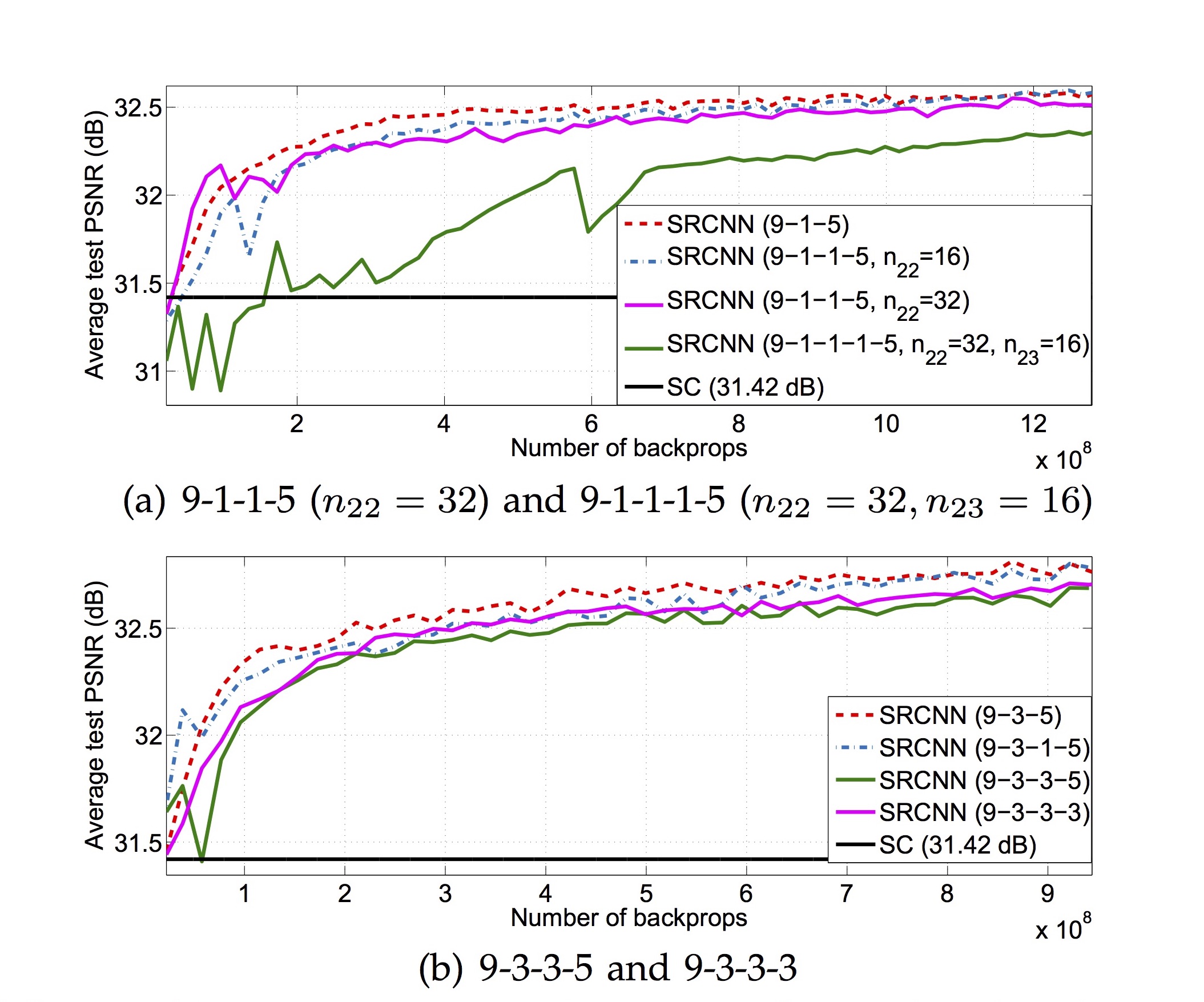
다음은 다른 SR 알고리즘들과 3배 확대한 결과물을 비교하는 그림입니다. 이 실험에는 filter size $f_1 = 9$, $f_2 = 5$, $f_3 = 5$을 사용했으며, filter 개수는 $n_1 = 64$, $n_2 = 32$를 사용했고 ImageNet으로 training했습니다.

이 논문의 의의를 정리하면 다음과 같습니다.
- 기존 sparse-coding-based 방법을 일반화한 방법을 단순한 CNN 구조로 제시
- SR 문제에 deep learning을 최초 적용
- 모델 자체의 독창성은 높지 않지만 향후 연구에 지대한 영향
– Jamie;
References
- Chao Dong의 논문 “Image Super-Resolution Using Deep Convolutional Networks”
- 전태균 님의 슬라이드 “Image Super-Resolution Using Deep Convolutional Networks”
- Prudhvi Raj의 슬라이드 “Deep Learning for Image Super Resolution”
- CUHK의 SRCNN 프로젝트 홈페이지 “Image Super-Resolution Using Deep Convolutional Networks”
- Wikipedia의 Rectifier (neural networks)
- C.Y. Yang의 논문 “Single-image super-resolution: A benchmark”
- J. Yang의 논문 “Image Super-Resolution as Sparse Representation of Raw Image Patches”
- Stanford의 ImageNet dataset